Creative Output

On our road trip across the USA, Joey Marianer and I stayed at many Holiday Inn Express hotels. I noticed that (at least for the Eastern side of the country) they had a lot of geometrical decor. In particular, some intriguing wallpaper, which I will analyse in the second hald of the post.

But first, some other geometrical art. For instance, this art made of triangles, shown here with a copy of the book I read on the trip, Matt Parker’s ‘Love Triangle‘:

This art featuring hexagons, and occasional quadrilateral half-hexagons:

And this art with triangles inside hexagons!

This door decorated in triangles, diamonds, and parallelograms:

This more abstract collection of overlapping quadrilaterals making the occasional triangle:

Then there are perhaps less-artistic tesselations which I might not have noticed if not for the other decor. For instance, this couch featuring two different kinds of triangle:

This floor which seems to have at least two different lengths of floorboard:

This bedspread tesselation of diamonds and parallelograms:

Now, onto the wallpaper. This was present in many different Holliday Inn Express hotels. Here’s the photo I took:

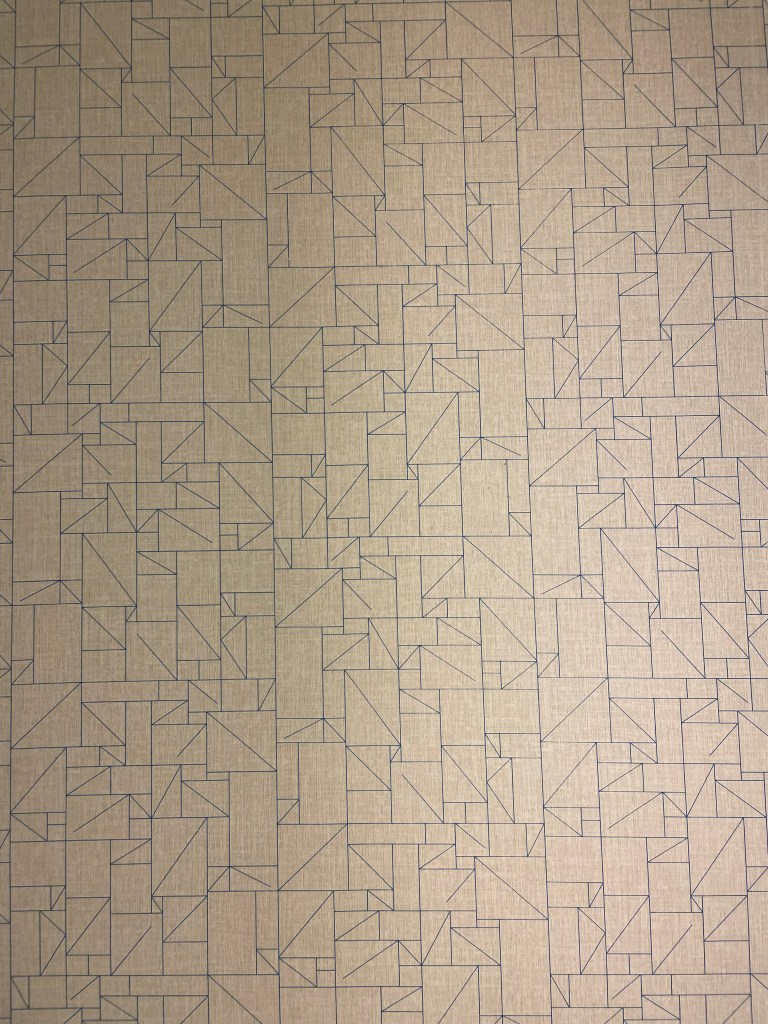
Here it is after I unskewed, cropped, and lightened it in GraphicConverter:

This raises a lot of questions:

1. What is the repeating unit here?
2. Which wallpaper group is it?
3. What’s with all those lines that don’t meet the other side? Would the pattern make any more sense if I completed them?
4. Is there some kind of pattern to the way the rectangles, the rectangles divided into triangles, and the rectangles with unfinished lines in them are arranged?

Okay, to answer the first question, here I’ve cropped it to show enough of the repeating units to recreate the whole thing, and converted it to black and white so we’re not distracted by the lighting:

At this point I switched from GraphicConverter to OmniGraffle. Here I’ve drawn in the repeating tiles:

There are two kinds of tile, which I’ve outlined in solid purple and dashed orange. Vertically, the two kinds of tile alternate. Each column of tiles is offset vertically by half a tile from the ones next to it, so if you follow across the wallpaper, you’ll be alternating between top and bottom halves of tiles, and they might all be the same kind of tile, or they might be alternating kinds of tile, depending on where you start.

It took me a while to realise (actually, I think Joey pointed it out), but the orange tile is in fact the same as the purple tile, just flipped horizontally. That means we have what’s called a glide symmetry, or glide reflection — it’s like a reflection, but the reflection is moved along. The classic example of a glide symmetry is a trail of footprints — the two feet are mirror images of each other, but since they were walking when they made the footprints, they are never exactly next to each other.

So that means we can answer the question about wallpaper groups. It’s a rectangular lattice with only glide symmetries, no rotations or reflections. That’s called pg, and you can see other examples of it on wikipedia.

Here’s a single tile of it, from which we can construct the whole wallpaper:

It has 43 triangles (mostly in rectangles divided into two triangles, but there’s one divided into three triangles on the bottom left), 24 plain rectangles, and 5 rectangles that have a diagonal line going partway across them.

Okay, so onto question three. What’s with those lines that don’t quite reach the other side? Here, I completed them, and approximately measured the angles using the arc tool in OmniGraffle (I use OmniGraffle for a lot of things that aren’t graphs. For instance, this quark explainer, and the icon of my next app.)

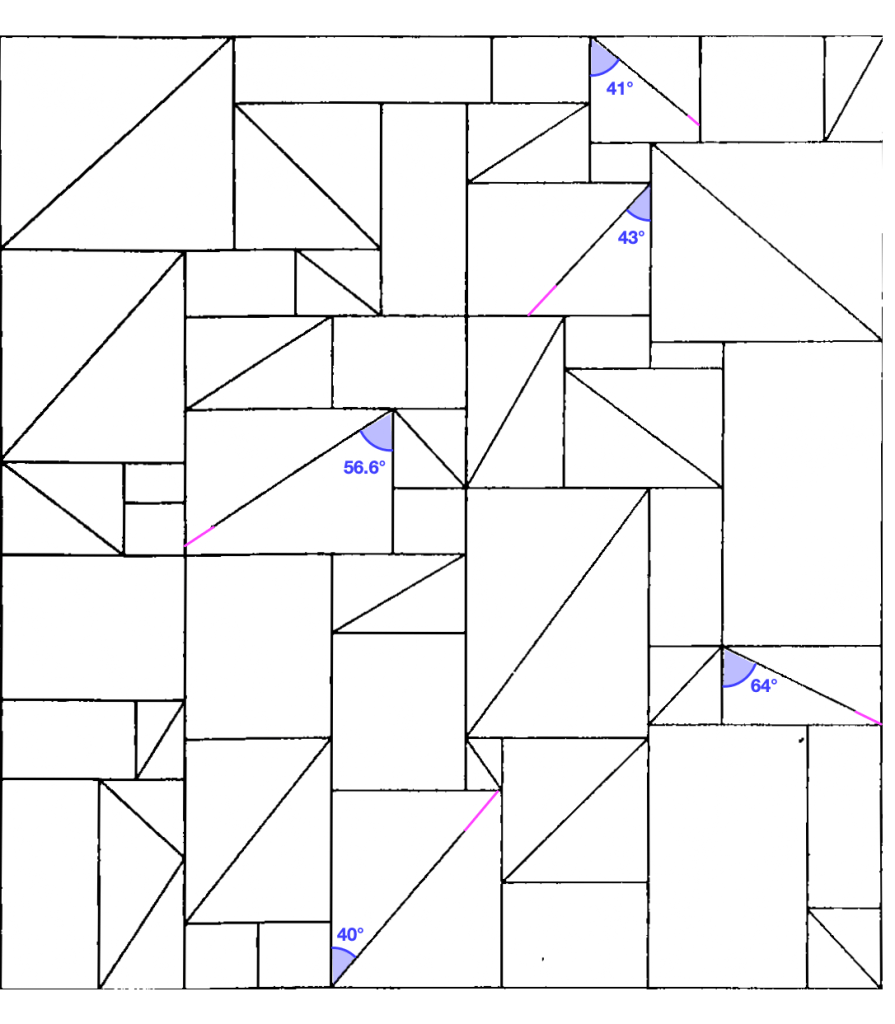
There. Is that enlightening? No. Is that satisfying? Also, no. Two of the lines pretty much reach the other corner, if you squint, and three of them don’t. But perhaps knowing that you can give up on making any sense of this will give some relief.

Ah, but what about the arrangements of the three kinds of rectangle? Surely there’s something interesting about that. I haven’t found it, but maybe you could. Here’s a single tile, with a purple rectangle pattern for the plain rectangles, a pink zigzag pattern for rectangles divided into triangles, and a green pattern of short lines for rectangles with maddening partial lines in them. I’m not sure how useful the redundant coding is here, but it can’t hurt.

I’m not sure why I didn’t colour the three-triangle rectangle near the bottom left in a different colour from the two-triangle rectangles. I made these a while ago. [Next day edit: This bothered me too much to ignore. See below for a version with a different colour for that rectangle.]

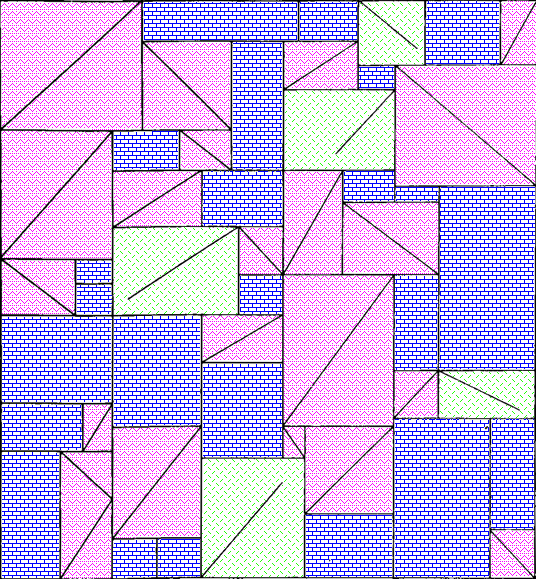
I can imagine the letter P and a dog standing on its hind legs in pink, but I don’t think there’s any kind of hidden message here. Just to be sure, here’s the colourised version extended to show more of the wallpaper:

Well now perhaps there are a bunch of dogs walking past each other doing the can-can. Do you see any interesting geometry or other mathematics that I missed in any of these images?

Next-day edit: Here’s a version with the three-triangle rectangle in checkered orange. I accidentally used a different shade of pink, but the shade of pink had no mathematical value, so it’ll do:

And here’s a larger section of wallpaper using that version:

When I took these photos, I thought they might make a good talk at the MathsJam Annual Gathering. We ended up deciding not to go this year (though we’ll probably join virtually) so I won’t be giving that talk. I have also made a new app which could be the focus of a MathsJam talk. I have submitted it to the App Store, so I hope it will be out very soon.

On the subject of apps, I got a job offer, though I haven’t started work yet. That means I’ve released a new version of Seddit, my text-to-speech-focused Reddit reader, where the only update is that it no longer says I’m looking for work on the ‘Support Seddit’ tab of the settings.