Archive for October, 2025
Arithmancy Pants for macOS and iOS: Because everything’s a magic number if you’re brave enough
Posted by Angela Brett in My Software on October 31, 2025
TL;DR: I made an app to derive a lot of ‘lucky’ numbers from any text. You can get it on the App Store now, for iOS and macOS.
Many years ago I came across Uri Geller’s page about how he notices the number 11 a lot and it’s somehow a magic number. I didn’t read all of it, because it’s nonsense, but I was intrigued by the list of ‘Names, events and places that add up to 11 letters.’ It contains:
- Many words, names, and phrases that happen to have 11 letters
- The words ‘hell heaven’ that sound a bit like 11
- Events that happened on the 11th of some month, or in November, or at 11:11
- The fact that Queen Elizabeth II is often written EIIR, which looks like E11R (of course, if you know Roman numerals, it clearly means E2R, but when I was a little kid I thought the Commodore 64 game Saboteur II was Saboteur 11, so I shouldn’t judge)
- Numbers whose digits add up to 11, if you keep adding the digits of the result until you get to 11
- Dates whose digits add up to 22, if you keep adding the digits of the result until you get to 22
- Phrases that have two consecutive As in them (because A is the first letter of the alphabet)
- Numbers that have two or more consecutive 1s in them
- Numbers that have two or more non-consecutive 1s in them, separated by zeroes
- Numbers that have 2 in them
It was clear to me that if you look hard enough, you can find 11s anywhere. Not only that, but you could find whatever other smallish (under 1000 or so) numbers you’re looking for. So I wrote code to look for a lot of these things automatically, and put it in an iOS and macOS app called Arithmancy Pants. It’s called that because ‘Numerologist’ was taken, arithmancy is an older word for numerology, and I’m a two-time Fancy Pants Parade winner.
I broke down everything into independent steps, so that we can find as many numbers as possible without doing the same thing twice — for instance, instead of converting AA to 11, we first convert it to 1, 1, and then concatenate them in a separate step to make 11.
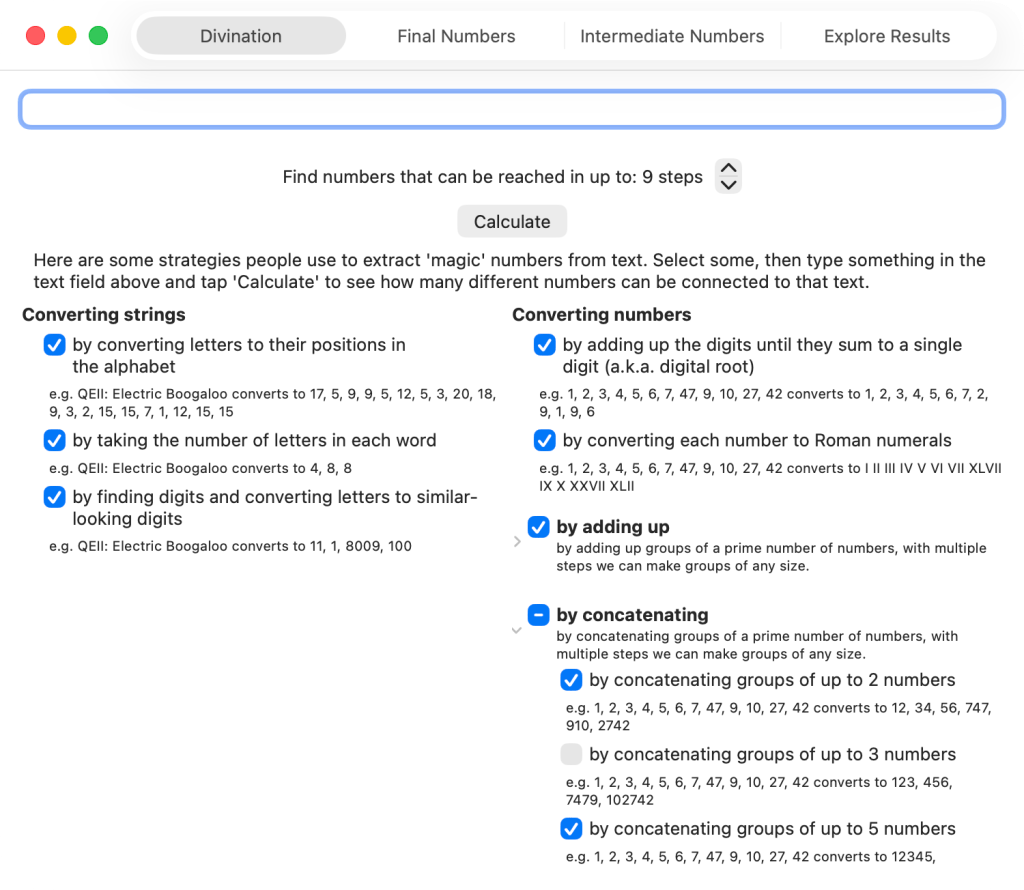
Here are the things Arithmancy Pants can do in its quest to find numbers:
- Convert text into numbers
- by converting letters to their positions in the alphabet — Uri only uses this one for converting A to 1, but I’ve seen it quite often elsewhere
- by taking the number of letters in each word — this covers all the 11-letter words, and when combined with ‘adding up all the numbers’, covers other names and phrases with 11 total letters.
- by finding numbers that are already in the text, and letters that look like numbers — this covers the EIIR example.
- Convert numbers into other numbers
- By adding up the digits until they sum to a single digit (also known as digital root, this is equivalent to finding the remainder when dividing the number by 9, except using 9 instead of 0 unless we started at 0.)
- By converting each number into Roman Numerals — I think I only added this because I’d already written code to do that for something else. However, this covers the ‘numbers that have 2 in them’ case, as we can convert 2 to 11 by converting it first to II, and then to 11 by converting letters that look like numbers. This is a much more manageable way of turning 2 to 11 than adding a generic ‘convert each number into every possible combination of numbers that add to that number’ step.
- By adding up numbers
- Adding up all the numbers — this covers most of the adding-up cases on Uri’s page
- Adding up numbers in groups of up to 2, 3, 5, 7, and 11 numbers. By using prime-sized groups, in multiple steps we can add the numbers in groups of any size — e.g., we can add up groups of 6 numbers by first adding groups of 3 numbers, then adding those results in groups of 2.
- By concatenating numbers — combined with converting letters to their positions in the alphabet, this covers converting AA to 11
- Concatenating all the numbers
- Concatenating numbers in groups of up to 2, 3, 5, 7, and 11 numbers.
I stop at combining groups of 11, because while I could handle even larger numbers internally by using a different data type:
- I’ve got to stop somewhere, and not many people’s supposed lucky numbers have enough digits for concatenations or sums of multiples of 13 numbers to matter.
- I show charts of the numbers found, and there seems to be a bug (FB20491693, if you’re at Apple) in Swift Charts when I include more than one result that would convert to the same
Doublevalue. So I’m limited to final numbers under 253. - 13 is an supposedly an unlucky number anyway.
The app shows the final numbers you get when you complete enough of these steps to get down to a single number. On another tab it shows the intermediate numbers found alongside other numbers partway through the process. You can also explore the results yourself by expanding each intermediate result to see what was derived from it in the next step.
Note, there were many years between when I saw that page and when I actually wrote the app. So I don’t cover:
- Words that sound like numbers. I could have easily done something like this, at least on macOS, as I have a lot of experience with the text-to-speech APIs, but I simply forgot that was one of the tactics. Actually, I would probably just have a list of known words (too, to, for, non-rhotic Severn, etc.) that sound like numbers, or perhaps I would derive such a list by searching through a lot of text using the text-to-speech API. Uri’s suggestion of ‘hellheaven’ would not have come up though, since it doesn’t actually sound like eleven.
- Numbers that have consecutive or non-consecutive ones in them… although, this depends on how we got the numbers. If we obtained 10001 by concatenating 10, 0, 0, and 1, we would also have added those numbers to get 11.
- Stopping halfway when calculating the digital root — e.g., adding up the digits of 254 to get 11, but not continuing to add up the digits in 11 to get 2. I just take the remainder when dividing by nine to do the whole thing in a single step, so this won’t even be shown in the intermediate values.
I think that’s all I have to say about that… as I mentioned in my last post, this could also be a MathsJam talk some day. You can download the app for free on any device running macOS 26 or iOS 26. You could use it to debunk the claims of numerologists, or to make your own claims for fun — but please don’t use it to take advantage of gullible people.
Holiday Inn Express Geometry
Posted by Angela Brett in News on October 26, 2025
On our road trip across the USA, Joey Marianer and I stayed at many Holiday Inn Express hotels. I noticed that (at least for the Eastern side of the country) they had a lot of geometrical decor. In particular, some intriguing wallpaper, which I will analyse in the second hald of the post.
But first, some other geometrical art. For instance, this art made of triangles, shown here with a copy of the book I read on the trip, Matt Parker’s ‘Love Triangle‘:

This art featuring hexagons, and occasional quadrilateral half-hexagons:

And this art with triangles inside hexagons!

This door decorated in triangles, diamonds, and parallelograms:

This more abstract collection of overlapping quadrilaterals making the occasional triangle:

Then there are perhaps less-artistic tesselations which I might not have noticed if not for the other decor. For instance, this couch featuring two different kinds of triangle:

This floor which seems to have at least two different lengths of floorboard:

This bedspread tesselation of diamonds and parallelograms:

Now, onto the wallpaper. This was present in many different Holliday Inn Express hotels. Here’s the photo I took:
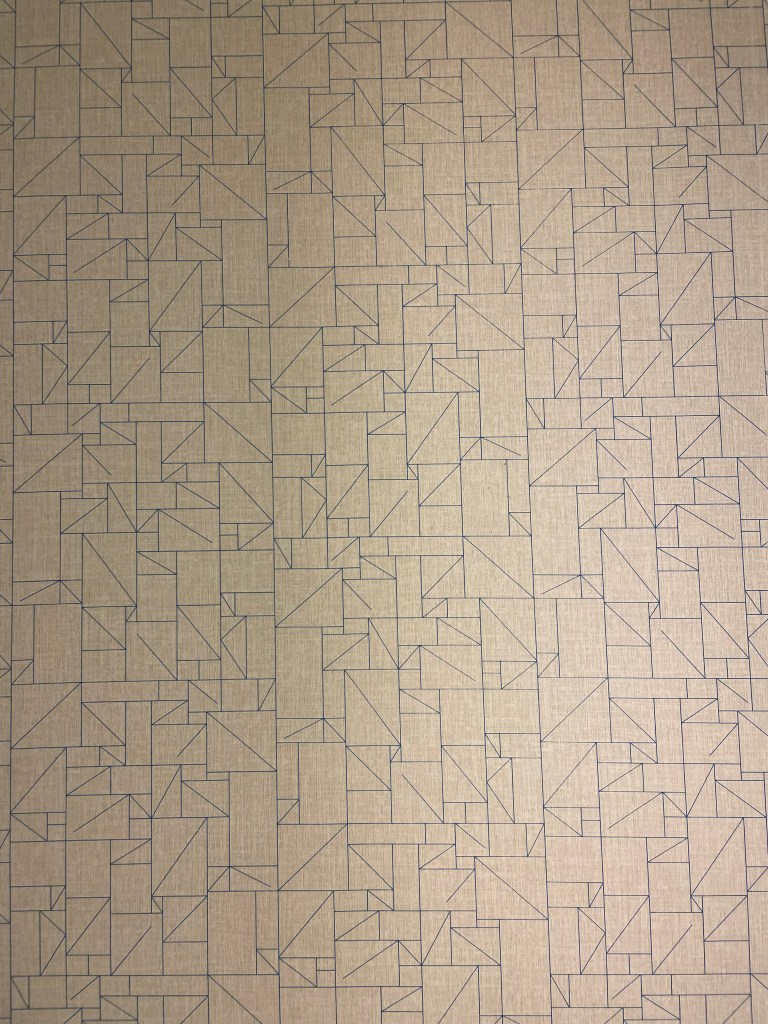
Here it is after I unskewed, cropped, and lightened it in GraphicConverter:

This raises a lot of questions:
- What is the repeating unit here?
- Which wallpaper group is it?
- What’s with all those lines that don’t meet the other side? Would the pattern make any more sense if I completed them?
- Is there some kind of pattern to the way the rectangles, the rectangles divided into triangles, and the rectangles with unfinished lines in them are arranged?
Okay, to answer the first question, here I’ve cropped it to show enough of the repeating units to recreate the whole thing, and converted it to black and white so we’re not distracted by the lighting:

At this point I switched from GraphicConverter to OmniGraffle. Here I’ve drawn in the repeating tiles:

There are two kinds of tile, which I’ve outlined in solid purple and dashed orange. Vertically, the two kinds of tile alternate. Each column of tiles is offset vertically by half a tile from the ones next to it, so if you follow across the wallpaper, you’ll be alternating between top and bottom halves of tiles, and they might all be the same kind of tile, or they might be alternating kinds of tile, depending on where you start.
It took me a while to realise (actually, I think Joey pointed it out), but the orange tile is in fact the same as the purple tile, just flipped horizontally. That means we have what’s called a glide symmetry, or glide reflection — it’s like a reflection, but the reflection is moved along. The classic example of a glide symmetry is a trail of footprints — the two feet are mirror images of each other, but since they were walking when they made the footprints, they are never exactly next to each other.
So that means we can answer the question about wallpaper groups. It’s a rectangular lattice with only glide symmetries, no rotations or reflections. That’s called pg, and you can see other examples of it on wikipedia.
Here’s a single tile of it, from which we can construct the whole wallpaper:

It has 43 triangles (mostly in rectangles divided into two triangles, but there’s one divided into three triangles on the bottom left), 24 plain rectangles, and 5 rectangles that have a diagonal line going partway across them.
Okay, so onto question three. What’s with those lines that don’t quite reach the other side? Here, I completed them, and approximately measured the angles using the arc tool in OmniGraffle (I use OmniGraffle for a lot of things that aren’t graphs. For instance, this quark explainer, and the icon of my next app.)
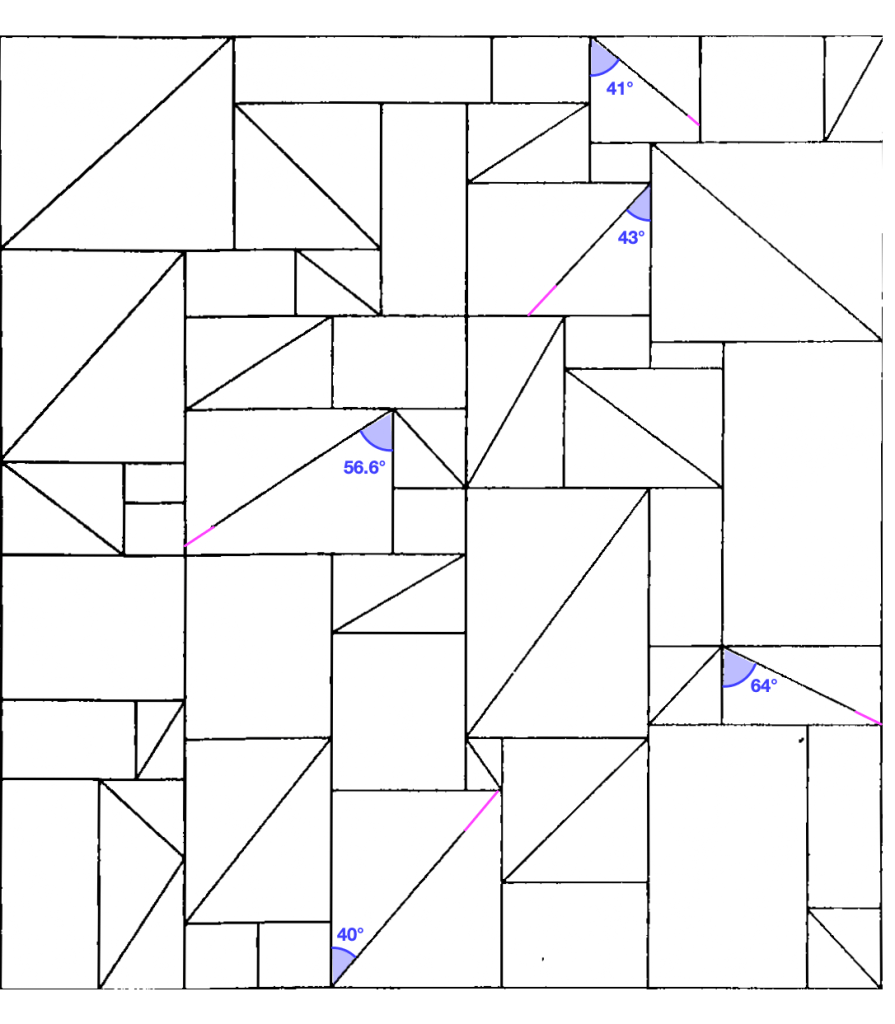
There. Is that enlightening? No. Is that satisfying? Also, no. Two of the lines pretty much reach the other corner, if you squint, and three of them don’t. But perhaps knowing that you can give up on making any sense of this will give some relief.
Ah, but what about the arrangements of the three kinds of rectangle? Surely there’s something interesting about that. I haven’t found it, but maybe you could. Here’s a single tile, with a purple rectangle pattern for the plain rectangles, a pink zigzag pattern for rectangles divided into triangles, and a green pattern of short lines for rectangles with maddening partial lines in them. I’m not sure how useful the redundant coding is here, but it can’t hurt.
I’m not sure why I didn’t colour the three-triangle rectangle near the bottom left in a different colour from the two-triangle rectangles. I made these a while ago. [Next day edit: This bothered me too much to ignore. See below for a version with a different colour for that rectangle.]
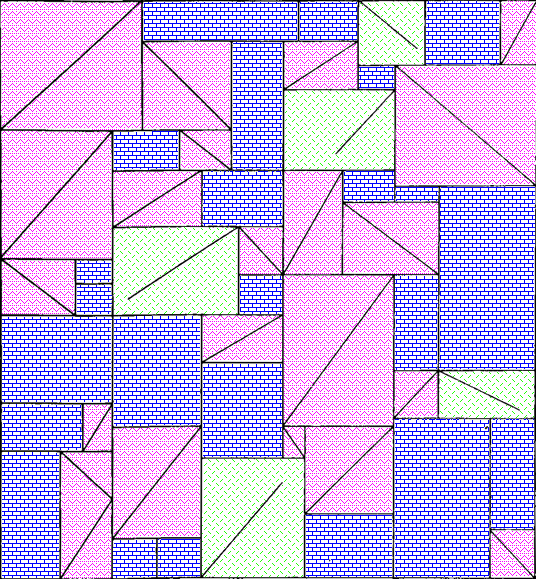
I can imagine the letter P and a dog standing on its hind legs in pink, but I don’t think there’s any kind of hidden message here. Just to be sure, here’s the colourised version extended to show more of the wallpaper:

Well now perhaps there are a bunch of dogs walking past each other doing the can-can. Do you see any interesting geometry or other mathematics that I missed in any of these images?
Next-day edit: Here’s a version with the three-triangle rectangle in checkered orange. I accidentally used a different shade of pink, but the shade of pink had no mathematical value, so it’ll do:

And here’s a larger section of wallpaper using that version:

When I took these photos, I thought they might make a good talk at the MathsJam Annual Gathering. We ended up deciding not to go this year (though we’ll probably join virtually) so I won’t be giving that talk. I have also made a new app which could be the focus of a MathsJam talk. I have submitted it to the App Store, so I hope it will be out very soon.
On the subject of apps, I got a job offer, though I haven’t started work yet. That means I’ve released a new version of Seddit, my text-to-speech-focused Reddit reader, where the only update is that it no longer says I’m looking for work on the ‘Support Seddit’ tab of the settings.
Seddit 1.5 supports multilingual Reddit listening. Also, Joey sang my half-baked PSOLA song!
Posted by Angela Brett in My Software on October 9, 2025
A while ago I added the possibility to configure Seddit (my text-to-speech-focused hands-free Reddit client for macOS and iOS) with multiple voices so that each user’s content could be read in a different voice. Of course, iOS and macOS come with voices that speak a huge variety of different languages, so you could theoretically select, say, a Japanese voice, a French voice, and three English voices, and download Reddit posts and comments in all of those languages. However, until now, Seddit would randomly assign a voice to each user, without regard for the language that user had written in, so if you did that, you could end up with English posts pronounced as if they were French, Japanese character names read out in English, and so on.
In the latest version, if you select voices that speak multiple languages in the Voices tab of the Settings screen, when Seddit encounters a post or comment by a user it hasn’t chosen a voice for yet, it will detect which of those languages the post or comment is probably in, and choose a voice that knows how to pronounce that language.
Of course, this isn’t perfect — it still always uses the same voice for each user, so if a user sometimes posts in French, and sometimes in English, or if they write in multiple languages within a single post because it’s a language-learning subreddit, then some of that is going to be spoken using an inappropriate voice. Also, if someone only writes in English but the first comment that Seddit encounters of theirs is an image meme and the text ‘c’est la vie!’ Seddit might determine that the user speaks French, and then hilariously mispronounce the rest of their posts. Note, if there is not enough text in the user’s first post for Seddit to even guess the language, it will not definitively choose a voice for that user until it encounters another post by them. I have yet to find either of these situations in practice, even while looking for them, so I hope it’s a rare issue.
Nonetheless, all of these situations are better than Seddit just randomly picking a voice for each user, regardless of which language they happen to be writing in. You should try it out, especially if you want to listen to Reddit content in various languages!
I also redesigned the Settings screen on iOS and iPadOS so it’s fullscreen and has a close button in the top right, as per Apple’s human interface guidelines, instead of a ‘Done’ button taking up a lot of space at the bottom and making the tabs look weird.
Note, while writing this post, I tested the regular ‘Start Speaking’ menu command on macOS and the ‘Speak’ command on iOS and found that it will sometimes switch to appropriate voices if I select multilingual text, even if my System Speech Language est réglé sur えい語。 Okay, it doesn’t work well for the French/English parts of that sentence. Maybe it’s only good with switching between languages if I switch scripts, e.g. בַּרְוָזָן утконос カモノハシ. Yep, that works, although if I select any other text along with πλατύπους, it’ll read it as ‘Greek small letter pi’ etc. I guess Greek letters are used too often in English for the speech engine to assume we actually switched to Greek. There were certainly plenty of Greek letters in the Princeton Companion to Mathematics.
Anyhow, I’m thinking I could improve Seddit further by giving each user a voice in each language you’ve selected voices for, and detecting the language for each post/comment, or for each sentence. Though macOS doesn’t do that unless you switch scripts… when I tried adding ‘J’imagine qu’il choisit une nouvelle langue pour chaque phrase.’ as a separate sentence and selected it along with a few English sentences, it read the whole thing in a French voice.
On the subject of interesting text-to-speech behaviour, and interesting behaviour in general, remember my half-written Lola parody about Pitch Synchronous Overlap and Add? Well, the lovely Joey Marianer had an appointment in town a while ago, and sneakily recorded the song in a parking building as a surprise, because I’m usually home so there’s little chance to record things at home without my hearing. I was duly surprised and delighted. Even the disclaimer about the missing bridge sounds like it scans as a bridge! Now you can also be surprised, delighted, and probably confused as to why this half-baked song was considered worth singing.